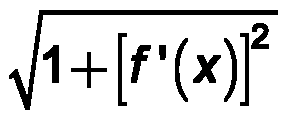---

Themen für Referate im Leistungskurs

12. Klasse - Infinitesimalrechnung 

	zurück zu Mathematik 12. Klasse
	Hinweise für das Anfertigen von Referaten (nicht nur in Mathematik)
1.	Das Integral in der Physik - Arbeitsintegral	[1] S. 233 - 234 [2] S. 84 - 85 [3] S. 27 - 29	Definition von "Arbeit" = Kraft ⋅ Weg Problem bei veränderlicher Kraft (Beispiel!) Entwicklung einer allgemeinen Definition $$ W=\int F(s)\cdot ds$$ evtl. konkretes Beispiel
2.	Das Integral in der Physik - Bewegungsgleichungen	[1] S. 231 - 232 [3] S. 30 [2] S. 81 - 83	Wiederholung der Bewegungsgleichungen (11. Klasse) Geschwindigkeit = Ableitung des Ortes nach der Zeit Beschleunigung = Ableitung der Geschwindigkeit nach der Zeit Umkehrung: $$ \mathrm{<br>\; W}eg=\int v(t)\cdot dt$$ ; $$ Geschwindigkeit=\int a(t)\cdot dt$$ evtl. konkretes Beispiel (freier Fall?)
3.	Berechnungen von Mittelwerten mit Hilfe der Integralrechnung	[3] S. 31 [2] S. 87 - 88	Beispiel für eine einfache Mittelwertberechnung (z. B. Durchschnittsnote) Durchschnitt bzw. Mittelwert bei Funktionen ("mittlerer Funktionswert") allgemeine Form des Mittelwerts evtl. konkretes Beispiel (z. B. Mittelwert von sin2x; Temperaturkurve o. ä.)
4.	Volumen von Rotationskörpern	[3] S. 32 - 34 [2] S. 95 - 97 [4] N.8.1, N.8.2	Problematik der Volumenberechnung bei Rotationskörpern Vorstellung der "Scheibenmethode" (vgl. "Streifenmethode" bei der Flächenberechnung) Beispiele
5.	Die Länge einer Kurve	[2] S. 98 - 99	allgemeines Problem Herleitung der allgemeinen Lösung Problematik der Integration von  evtl. konkretes Beispiel
6.	Anwendung der Exponentialfunktion (I) - Allgemeines Wachstumsgesetz, Entwicklung der Weltbevölkerung	[1] S. 278 [3] S. 91 - 94 [4] N.5.4	Bevölkerungsentwicklung, Vergleich mit einer Exponentialfunktion Grenzen (vgl. Aufgabe 3) Problematik bei weiterem Bevölkerungswachstum
7.	Anwendung der Exponentialfunktion (II) - Stetige Verzinsung	[3] S. 33 - 34 [4] N.5.3	Verzinsung, Zinseszinsen Kapitalzuwachs bei unterschiedlicher Verzinsung stetige Verzinsung
8.	Logarithmusfunktion in der Physik - Radioaktiver Zerfall	[1] S. 278	Zerfallsgleichung Halbwertszeit Problematik des radioaktiven Zerfalls (wann ist die Strahlung auf 1/2, 1/4, 1/10, ... des Anfangswerts zurückgegangen?) evtl. C14-Methode zur Altersbestimmung

nach oben

13. Klasse - Analytische Geometrie

9.	Abstände	[5] S. 204-207	Länge eines Vektors Abstand Punkt - Gerade
10.	Winkel	[5] S. 210-212	Skalarprodukt Winkel zwischen Vektoren orthogonale Vektoren
11.	Abstände zwischen Geraden	[5] S. 226-229	Abstand paralleler Geraden Abstand windschiefer Geraden
12.	Schnittwinkel zwischen Geraden	[5] S. 214-215, S. 225-226	Winkel zwischen Geraden Normalenvektor
13.	Kreis- und Kugelgleichung	[5] S. 278, 280	Kreisgleichung Kugelgleichung Beispielaufgabe
14.	Tangenten und Tangentialebenen	[5] S. 286-287, 289-290, 292	Kugel und Geraden Kugel und Ebenen

nach oben

13. Klasse - Wahrscheinlichkeitsrechnung

15.	Simulation von Bernoulli-Ketten	[6] S. 246-248	Galton-Brett Computersimulation
16.	Das Bernoullische Gesetz der großen Zahlen	[6] S. 261-264	Anwendung der Tschebyschew-Ungleichung auf Bernoulli-Ketten Veranschaulichung
17.	Testen von Hypothesen (1)	[6] S. 329-336 (auszugsweise!)	Alternativtest
18.	Testen von Hypothesen (2)	[6] S. 340-344	Signifikanztest

Literatur:

(z.T. beim Kursleiter erhältlich)